2023. 4. 12. 23:16ㆍ컴퓨터구조
1. Integer
Integer Addition
- 양수끼리 더하면 오버플로우 날 수 있음 -> 결과의 sign비트가 1이 되면 오버플로우
- 음수끼리 더하면 오버플로우 날 수 있음 -> 결과의 sign비트가 0이 되면 오버플로우
Integer Subtraction
- 양수에서 음수를 빼면 오버플로우 날 수 있음 -> 결과의 sign비트가 0이 되면 오버플로우
- 음수에서 양수를 빼면 오버플로우 날 수 있음 ->결과의 sign비트가 1이 되면 오버플로우
*그래픽과 미디어에서는 정해진 비트이상에서 캐리가 발생하면 그 캐리는 버린다.
-> Saturating operations :특정 범위 내에서 데이터 값의 정확도를 유지하기 위해
미리 정해진 범위내에서 오버플로우가 발생하면 그 결과는 버려서 제한
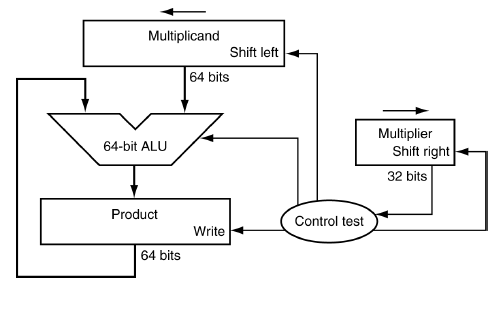
Multiplication Hardware
<로직>
1-1. 곱하는 수(Multiplier)가 1이면 Product(결과값)에 더하고 Product 레지스터에 저장
1-2. 0이면 더할 필요 없음
2. 다음 자리 계산 위해 Multiplicand(피제수)를 shift left 1 bit
3. Multiplier는 shift right 1 bit해서 다음 자리 수 곱하기
4. 32번 반복을 했다면 끝(32bit이므로). 아니면 다시 처음으로
-> O(n)번
Faster Multiplier
여러개의 adder를 사용하여 병렬적으로 계산-> 비용이 올라간만큼 성능 상승 -> 5번만에 연산 종료
-> O(log n)번

MIPS Multiplication
- 32bit 두개를 곱하면 결과는 최대 64bit가 되므로 32bit 레지스터 2개를 사용
- HI : 상위 32bit 저장 레지스터
LO: 하위 32bit 저장 레지스터 - 명령어
mult rs, rt / multu rs, rt
mfhi rd //HI에 저장되있는 걸 rd로 옮긴다.
mflo rd //LO에 저장되있는 걸 rd로 옮긴다.
(만약 32비트 안에 결과가 들어왔다면 HI레지스터 사용안해도 됨.)
mul rd, rs, rt //rs와 rt를 곱해서 rd로 저장(하위 32bit만 저장)
Division
1. divisor(나누는 수)가 0인지 확인
2. 나눗셈 진행
3. 나눗셈 진행 중 빼서 나머지가 0보다 작다면
-> 다시 divisor를 더해서 복구
* 부호있는 나눗셈 처리
-> 절대값을 취해서 계산 후 마지막에 몫과 나머지에 부호를 붙인다
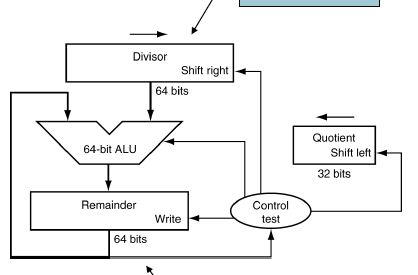
Division Hardware
<로직>
1. Remainder - Divisor 한 결과값을 Remainder 레지스터에 저장
2.
- Remainder가 0보다 크거나 같은 경우 나누어진 것이므로 몫을 shift left,
쉬프트한 자리에 비트는 1로 세팅
- Remainder가 0보다 작은 경우 나눌수 없는 것이므로
Divisor와 Remainder를 더해서 원래 값으로 복원한다. 몫은 shift left, 새로운 비트는 0으로 세팅.
3. Divisor를 다음 자리 계산 위해 shift right 1 bit
4. 33번 반복했는가 확인 -> 맞으면 종료, 아니면 1번으로 돌아간다.
MIPS Division
- HI : 32bit 나머지 저장 레지스터
LO: 32bit 몫 저장 레지스터 - 명령어
div rs, rt / divu rs, rt
mfhi, mflo 명령어를 통해 결과값 접근
2. Floating point
- normalized: (한자리수.유효숫자 )로 표현해야함.
- 표준: IEEE std 754-1985
- 두가지 표현방식이 있다
-> Single precision (32-bit)
Double precision (64-bit)

- S: sign bit
- 지정할 때 exponent는 실제 exponent + Bias
* Single: Bias = 127; Double: Bias = 1203 - Fraction- single에서 23비트 사용 가능 -> 10진수로 따지면 소수점 6~7번째자리까지 가능
double에서 52비트 사용 가능 -> 10진수로 따지면 소수점 16~17번째자리까지 가능
Single-Precision Range
- Exponent 00000000 과 1111111은 미리 특수한 수를 위해 예약되어 있다.
- 가장 작은 수: 1.0 × 2^(-126) ≈ 1.2 × 10^(-38)
Exponent: 00000001
-> actual exponent = 1-127 = -126
Fraction: 000…00
-> 1.0 - 가장 큰 수 : 2.0 × 2^ (+127) ≈ 3.4 × 10^(+38)
exponent: 11111110
-> actual exponent = 254 -127 = +127
Fraction: 111…11
-> ≈ 2.0
Double-Precision Range
single-precision에서 64비트로 바뀌었다는 점만 다르다. 계산은 알아서.
* 2진수로 소수점 나타내기
-> 0.1(2)는 10진수로 2^(-1)=1/2 -> 1.1(2)는 10진수로 1.5
0.01(2)는 10진수로 2^(-2)=1/4
0.001(2)는 10진수로 2^(-3)=1/8 .......
Floating-Point Addition
1. 자릿수 큰 거 기준으로 맞추기
1.000 × 2 ^(-1) + 1.110 × 2^(- 2)
-> 1.000 × 2 ^(-1) + 0.111 × 2 ^(-1)
2. 더하기
3. 결과값 Normalize하고, 오버플로우/언더플로우 났는지 체크
0.001 × 2^(-1)
-> 1.000 × 2^(-4)
4. Round(반올림) 해주고 필요하다면 renormalize
-> 유효숫자에 맞추기 위해 반올림
(유효숫자는 소수점의 길이가 더 짧은 거에 맞춘다.)
FP Adder Hardware
- 한 사이클안에 끝내게 만들려면 되게 오래걸린다.
- 더 늦게 끝나는 클럭이 모든 명령어들에게 페널티를 준다.
-> 클럭은 더 늦게 끝나는 거 기준으로 맞추기 때문. - 따라서 몇 사이클이 걸린다.
FP Instructions in MIPS
- FP 하드웨어는 보조 프로세서이다.
-> 별개의 FP 레지스터가 존재한다. - 32개의 single-precision용 레지스터 $f0 ~ $f31까지 존재
( double은 2개씩 묶어서 사용- ex) $f0/$f1, $f2/$f3 이렇게) - FP 명령어는 오직 FP 레지스터만 사용 가능
- 32bit용- load 명령어: lwc1
store 명령어: swc1 - 64bit용 - load 명령어: ldc1
store 명령어: sdc1
FP Example
float f2c (float fahr) {
return ((5.0/9.0)*(fahr-32.0));
}
# fahr in $f12, result in $f0, literals in global memory space--> MIPS Code
f2c:
lwc1 $f16, const5($gp) # 전역 메모리에서 상수5를 가져와서 $f16 레지스터에 load
lwc2 $f18, const9($gp)
div.s $f16, $f16, $f18
lwc1 $f18, const32($gp)
sub.s $f18, $f12, $f18
mul.s $f0, $f16, $f18
jr $ra
#32bit 명령어는 명령어 뒤에 .s를 붙힌다
# X = X + Y ×Z
# All 32 ×32 matrices, 64 bit double precision elements
void mm (double x[][],double y[][], double z[][]) {
int i, j, k;
for (i = 0; i! = 32; i = i + 1)
for (j = 0; j! = 32; j = j + 1)
for (k = 0; k! = 32; k = k + 1)
x[i][j] = x[i][j]+ y[i][k] * z[k][j];};
# Addresses of x , y , z in $a0, $a1, $a2, and
#i , j , k in $s0, $s1, $s2-> MIPS 코드
대체적으로 정수일때와 비슷
조금 다른 점만 코드로 남겨두겠음.
sll $t2, $s0, 5 # $t2 = i * 32 (size of row of x)
addu $t2, $t2, $s1 # $t2 = i * size(row) + j
sll $t2, $t2, 3 # $t2 = byte offset of [i][j] # double임으로 8 곱해야함
addu $t2, $a0, $t2 # $t2 = byte address of x[i][j]
l.d $f4, 0($t2) # $f4 = 8 bytes of x[i][j]연산을 병렬적으로 동시에 진행함
-> 예측하지 못한 순서로 뒤섞어서 연산 할 가능성 있음
'컴퓨터구조' 카테고리의 다른 글
| Chap 5- Memory(1) (0) | 2023.05.31 |
|---|---|
| Chap 4. Processor (2) | 2023.05.26 |
| 컴퓨터구조 전공수업 ch02 (1) | 2023.03.26 |
| 컴퓨터구조 전공수업 ch01. (0) | 2023.03.26 |
| CPU 캐시 메모리 (0) | 2023.03.21 |