4. 기계학습 - 학습 알고리즘

결정트리

: 트리 형태로 의사결정 지식을 표현한 것

• 내부 노드: 비교 속성
• edge: 속성값
• 단말 노드: 부류 또는 대표값

 

 

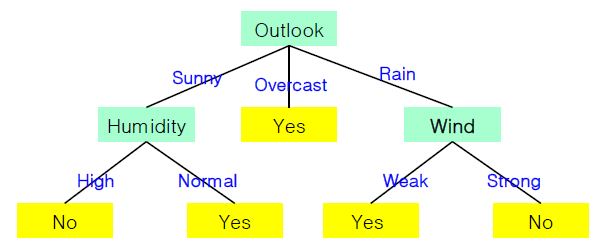
결정 트리 알고리즘

1. 모든 데이터를 포함한 하나의 노드로 구성된 트리에서 시작

2. 반복적인 노드 분할

1. 분할 속성을 선택
2. 속성값에 따라 서브트리를 생성
3. 데이터를 속성값에 따라 분배

 

어떤 분할 속성을 선택하는 것이 효율적인가?

-> 분할한 결과가 가능하면 pure(동질적)인 것으로 만드는 속성 선택

 

* 엔트로피

• 비동질 정도(불순도)를 측정하는 척도
• 섞인 정도(불순도)가 클수록 큰 값을 가진다.

 

 

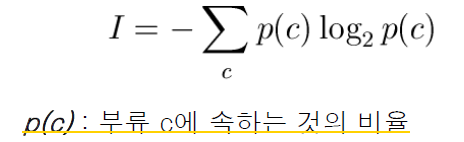
정보이득 (IG: Imformation Gain)

: 특정 속성으로 분할 한 후의 각 부분집합의 정보량의 가중평균

 

정보이득(IG)가 클 수록 우수한 분할 속성이다.

 

 

예) 부류 정보가 있는 데이터

다음과 같이 정보가 있을 때

 

엔트로피 계산

bits: 엔트로피 단위

 

 

Pattern 기준 분할 했을 때

 

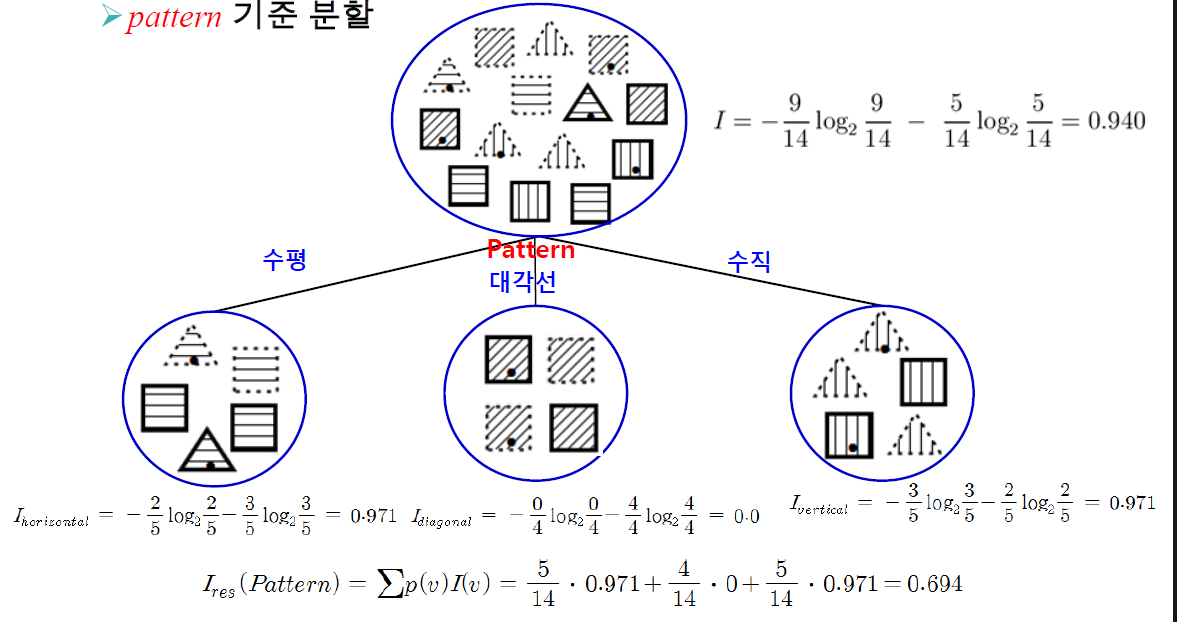
Pattern 속성에 대한 정보이득값

 

 

속성별 정보 이득

IG(Pattern)=0.246

IG(Outline)=0.151

IG(Dot)=0.048

-> pattern 속성값이 가장 크므로 선택

 

최종 결정트리

 

 

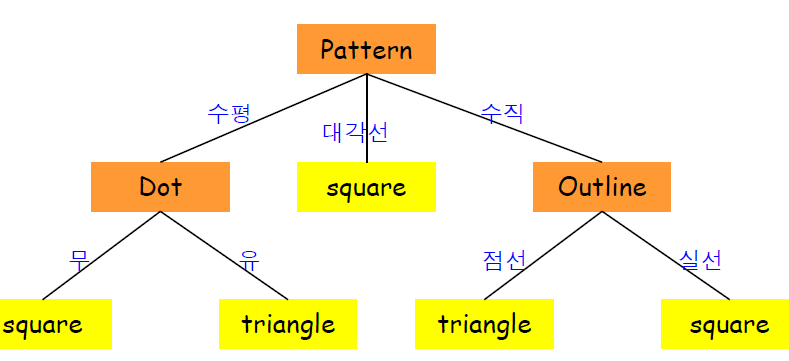
정보이득 척도의 단점

: 정보이득 척도는 속성값이 많은 것을 선호하는 방식이다.
-> 학번,이름같은 속성값을 선호하지만 이런 속성들은

새로운 데이터가 들어오면 분류하지 못한다.

 

이것을 개선하기 위한 척도

• 정보이득비
• 지니 지수

 

 

정보이득비(information gain ratio)

: 정보이득 척도를 개선한 것

-> 속성값이 많은 속성에 대해 불이익을 준다.

 

 

 

I(A): Intrinsic information

• 속성 A의 속성값을 부류로 간주하여 계산한 엔트로피
• 속성값이 많을 수록 커지는 경향을 갖는다.

 

 

예)

 

 

정보이득 VS 정보이득비

 

 

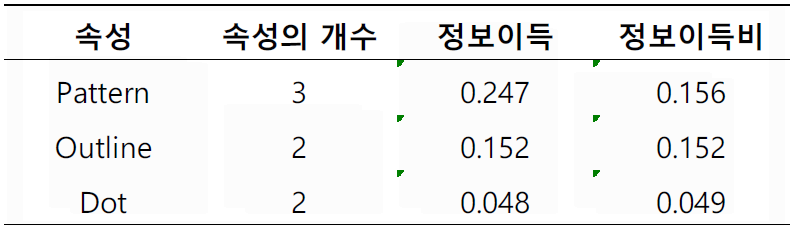
지니 지수(Gini index)

: 데이터 집합에 대한 Gini 값

 

i,j는 부류를 나타낸다.

예)

 

 

지니지수 이득(Gini index gain)

: GiniGain(A)=Gini - Gini(A)

 

속성 A에 대한 지니 지수값 가중평균

 

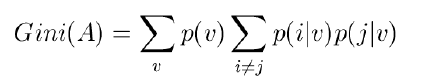
예)

 

 

분할속성 평가 척도 비교

 

 

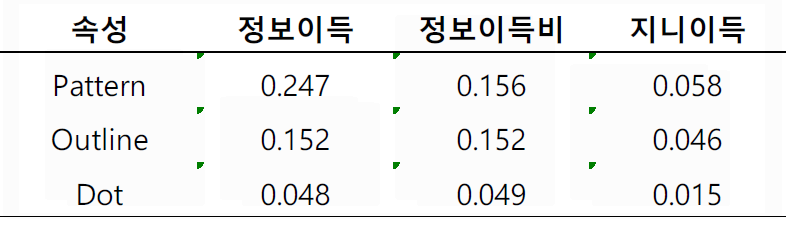
회귀를 위한 결정트리

회귀: 출력값이 수치값

 

 

분류를 위한 결정트리와 차이점

• 단말노드가 부류가 아닌 수치값 
  -> 해당 조건을 만족하는 것들의 대표값

 

분할 속성 선택

• 표준편차 축소 SDR을 최대로 하는 속성 선택

SDR(A)=SD - SD(A)

 

예)

다음과 같을 때

 

 

 

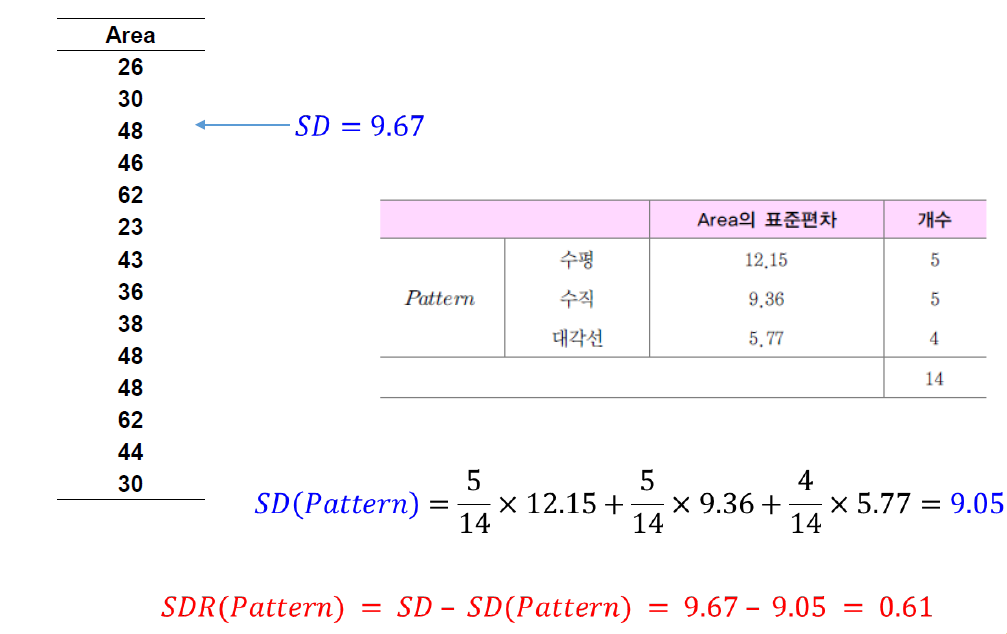
군집화 알고리즘

: 군집간의 유사도는 작게(거리는 크게), 군집 내의 유사도는 크게(거리는 작게) 분류하는 알고리즘

 

1. 계층적 군집화

• 군집들이 계층적인 구조를 갖도록
• 병합형(aggromerative) 계층적 군집화
  : 각 데이터가 하나의 군집을 구성하는 상태에서 시작.
  -> 가까이에 있는 군집들을 결합하는 과정을 반복하며 계층적인 군집 형성
• 분리형(divisive) 계층적 군집화
  : 모든 데이터를 포함한 군집에서 시작.
  -> 유사성을 바탕으로 군집을 분리하여 점차 계층적인 구조를 갖도록 구성

2. 분할 군집화

: 계층적 구조를 만들지 않고 유사한 것들끼리 나누어 그냥 묶는 것.

예) k-means 알고리즘

 

 

K-means 알고리즘

1. 군집의 중심위치 선정

2. 중심위치를 기준으로 군집 재구성

3. 군집별 평균 위치 결정

4. 군집 평균 위치로 군집 중심위치 조정

5. 수렴할 때(군집들이 변하지 않을 때)까지 2~4 반복

 

예)

1. 

2.

3~4.

군집 중심 위치를 군집의 평균 위치로 이동

5.

새로운 군집 중심을 기준으로 군집 재구성

군집 평균 재계산 후 군집 중심을 평균위치로 변경

 

 

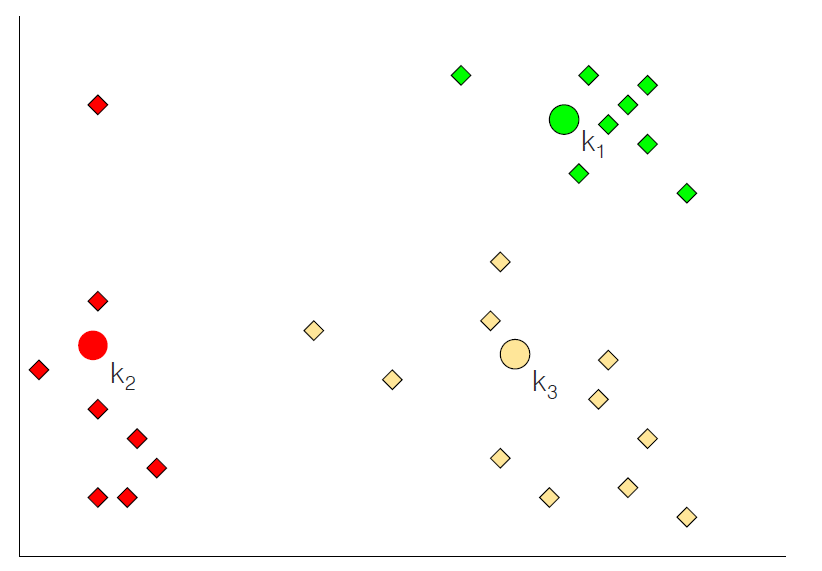
K-means 알고리즘 특징

• 분산값 V를 최소화하는 Si를 찾는 것이 알고리즘의 목표

i번째 군집의 중심을 ui, 군집에 속하는 점의 집합을 Si라 할 때, V는 전체 분산

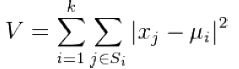
• 군집의 개수 k는 미리 지정
• 초기 군집 위치에 민감하다.

 

 

단순 베이즈 분류기

: 부류 결정지식을 조건부 확률로 결정

 

베이즈 정리

 

가능도의 조건부 독립 가정

 

예)

 

 

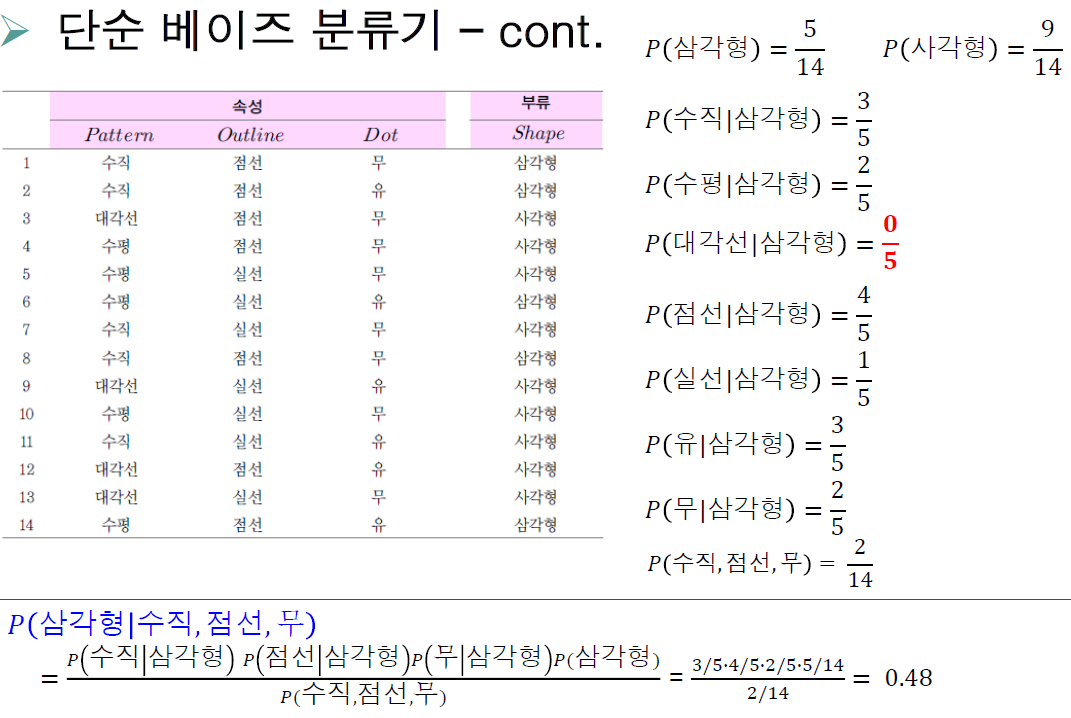
이렇게 확률을 구해서 더 큰 확률의 부류로 분류하도록 학습시킨다.