2024. 4. 16. 15:31ㆍ데이터베이스
좋은 설계 방법은
1. 중복을 피해야 하고
2. null값을 피해야 한다.
1. 중복을 피하기 위해선
-> 두 스키마로 Decomposition(분해) 하면 된다.
그러나 분해할 때 정보의 손실이 일어나서는 안된다. (Lossy decomposition)
분해한 테이블을 합쳤을 때 원본과 같아야 한다.

식으로 쓴다면
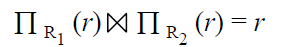

정규화하는 이유
1. 삽입 이상
2. 갱신 이상
3. 삭제 이상
위 3가지를 피하기 위함.
1차 정규화(1NF)
: 모든 속성들이 원자값을 가지도록 분해
-> 원자값: 더 이상 분해되지 않는 속성값을 가짐.
예)

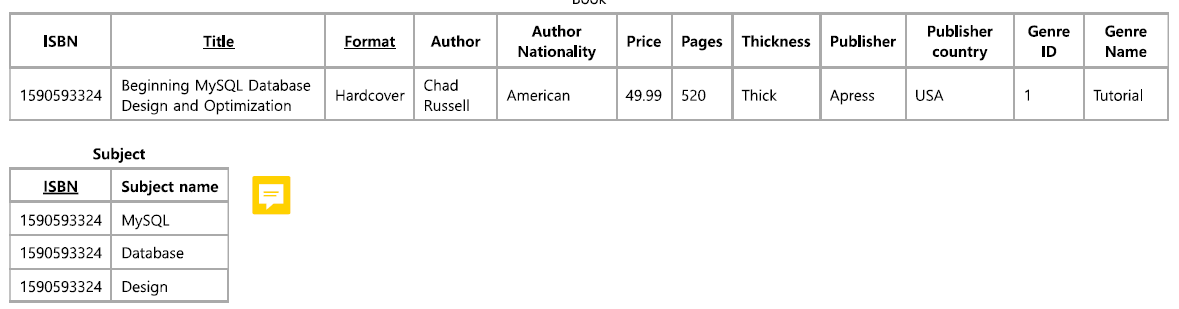
Functional Dependencies(함수 종속성)
1. 정의:
함수 종속성 X->Y는 릴레이션 R에서 튜플들이
X속성값이 같다면 Y속성값도 반드시 같다는 것을 의미.
즉, X값에 의해 Y값이 결정.

B -> A는 성립하지만 A-> B는 성립하지 않음.
1은 4일 수도 있고 5일 수도 있으므로
2. 사용:
- 함수 종속성은 데이터의 제약조건을 명시하는 데 사용
- 릴레이션 분해 시 lossless 분해를 위해 활용
3. 함수 종속성의 Closure(폐쇄):
어떤 함수 종속성 집합 F에 대해,
F+는 F에 의해 논리적으로 암시되는 모든 함수 종속성의 집합.
-> 이는 릴레이션 스키마의 키를 찾는 데 사용.
예) A -> B이고 B-> C이면 A-> C
4. 키와 함수 종속성:
슈퍼키: 릴레이션 R에서 K->R이 성립하는 속성집합 K
후보키: 슈퍼키 중 minimal 한 속성 집합

예를 들어 depth_name -> building 같은 경우 성립하지만
dept_name -> salary는 성립 불가.
-> 이를 통해 함수 종속성이 슈퍼키를 넘어 다양한 제약조건 표현가능.
Trivial Functional Dependencies
예) ID, name -> ID
name -> name
위의 예제처럼 함수 종속성이 자명한 걸 뜻함.
Lossless Decomposition
: decomposition(분해)이 손실(lossless)되지 않았는지 확인하기 위해
함수 종속성을 사용할 수 있다.


trivial 하거나 lossless Decomposition 하다면 functional dependencies 성립
예)
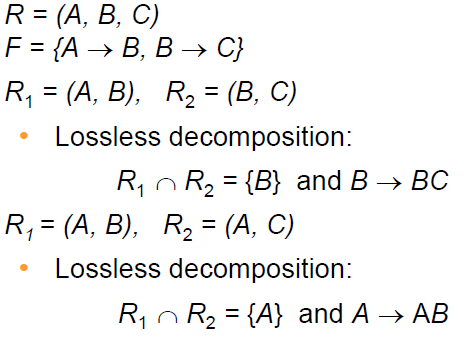
Dependency Preservation
종속성 보존: 함수 종속성 제약조건을 검사하기 위함
- 분해 후에도 원래 관계에 있던 함수 종속성을 효율적으로 테스트할 수 있어야 합니다.
- 즉, 특정 함수 종속성 X->Y를 검사하기 위해 여러 관계를 조인할 필요가 없어야 합니다.
* lossless decomposition이나 dependency preservation을 모두 만족하기 어려운 경우
둘 중 하나만 만족하도록 선택해야 한다.
-> 둘 다 만족하면 좋지만 어느 한쪽을 택하면 다른 한쪽은 성립되지 않기 때문.
예)

(A,B)와 (B, C)로 분해한 경우 조인하지 않아도 함수 종속성이 모두 보존되지만
(A, B)와 (A, C)로 분해한 경우 조인해야만 함수 종속성이 보존된다.
Boyce-Codd Normal Form
- a -> b가 trivial 하거나
- a가 슈퍼키라면
BCNF 성립.
예)

dept_name -> building, budget 이 함수 종속성은
trivial 하지도 않고
dept_name(학과이름)으로 각 행을 유일하게 식별할 수 없다.
-> 따라서 슈퍼키가 될 수 없다.
Decomposing a Schema into BCNF
BCNF에 맞게 분해하기
a -> b 함수 종속성이 있을 때
- a ∪ b 인 릴레이션 하나와
- R - (b-a) 릴레이션 하나로 분해하면 된다.
예)

BCNF and Dependency Preservation

BCNF와 종속성 보존을 동시에 만족시킬 수 없는 경우가 있다.
- i_ID는 후보키가 아니므로 BCNF를 만족하지 않는다.
-> i_ID는 교수번호로 유일하게 하나의 행을 구별할 수 없다. - BCNF로 만들기 위해서는 분해가 필요하다.
- 그러나 어떻게 분해하든 s_ID, dept_name -> i_ID 함수 종속성을 포함하는
스키마를 만들 수 없다.
Third Normal Form
- a -> b가 trivial 하거나
- a가 스키마 R의 슈퍼 키거나
- b-a에 속하는 모든 속성이 스키마 R의 후보키에 포함되어 있어야 한다.
BCNF의 조건보다 더 완화된 조건이다.
-> 3번 조건도 추가로 허용하기 때문.
예)

- trivial 한 함수 종속성은 없음
- s_ID, dept_name은 슈퍼키이지만
i_ID는 슈퍼키가 아님 - 그러나 dept_name - i_ID=dept_name이므로
후보키에 포함되어 있음 - 따라서 위 스키마는 3NF이다.
3NF의 장점
: 항상 종속성 보존(dependency preservation)과 무손실 분해를 만족할 수 있다.
3NF의 단점
: 분해 결과 일부 정보의 중복이 발생할 수 있다.
null값을 사용해야 하는 경우가 생긴다.
* BCNF와 장단점이 반대.
Goals of Normalization(정규화의 목표)
정규화의 목표
- 주어진 관계 스키마 R과 함수 종속성 집합 F에 대해서
R이 "좋은 형태(good form)"인지 판단하고
좋은 형태가 아니라면, {R1, R2,..., Rn}과 같이 R을 분해해야 한다.
1. 분해의 조건
- 각각의 Ri가 좋은 형태여야 한다.
- 분해가 무손실 분해(lossless decomposition)여야 한다.
- 가능하다면 종속성 보존(dependency preserving)도 만족해야 한다.
2. 좋은 형태의 기준
- 과거에는 BCNF(Boyce-Codd Normal Form)가 좋은 형태의 기준이었다.
- 하지만 BCNF로는 부족한 경우가 있어, 추가적인 정규형이 필요해졌다.
- 높은 수준의 정규형(4NF, 5NF 등)을 만족하면 이상 현상은 제거되지만,
테이블 수가 많아지고 조인 연산이 빈번해져 성능 이슈가 발생할 수 있다.
결론: BCNF로 종속성 보존은 포기하든
3NF로 종속성 보존은 지키되 정보의 중복성은 포기해야 한다.
'데이터베이스' 카테고리의 다른 글
| Hash Tables (0) | 2024.05.15 |
|---|---|
| 7. Storage (1) (0) | 2024.05.01 |
| 5. E-R model (0) | 2024.04.08 |
| 4. Modern SQL (1) | 2024.04.02 |
| 3. Intermediate SQL (2) | 2024.03.26 |