2024. 5. 15. 21:23ㆍ데이터베이스
쿼리 실행 엔진을 지원하기 위해
DBMS가 어떻게 페이지에서 데이터를 읽고 쓸까?
두 가지 유형의 데이터 구조가 있다.
1. 해시 테이블
2. 트리
테이블 설계에서 고려해야 할 두 가지
1. Data Organization
- 메모리/페이지에서 데이터 구조를 어떻게 배치할 것인지
- 효율적인 액세스를 지원하기 위해 어떤 정보를 저장할 것인지
2. Concurrency(동시성)
- 어떻게 다중 스레드가 데이터 구조에 동시에 접근할 수 있게 할 것인지
Hash Table
공간 복잡도: O(n)
시간 복잡도: 평균 O(1), 최악 O(n)
-> 데이터베이스는 상수 시간도 신경 써야 한다.
-> 최악의 경우를 방지하는 해싱 기법이 필요하다.
Static Hash Table
- 저장할 모든 요소에 대해 하나의 슬롯을 할당하는 거대한 배열을 할당
- 키를 해시한 값을 요소 수로 나눈 나머지
-> 즉, hash(key) % N을 배열의 offset으로 사용 - 이를 위해서는 다음 가정이 필요하다:
- 저장할 요소 수를 미리 알고 있어야 함
- 각 키가 유일해야 함(똑같은 키가 여러 개 있으면 안 됨)
- 완벽한 해시 함수여야 함 (다른 키는 다른 해시값)
-> 서로 다른 키에 대해서는 해시값이 달라야 한다.
이 세 가지 가정이 충족되지 않으면 정적 해시 테이블을 사용할 수 없다.
정적 해시 테이블은 요소 수와 테이블 크기를 미리 정해야 하는 제약이 있지만,
구현이 간단하다는 장점이 있다.
해시 테이블 설계 시 고려할 점
1. 해시 함수 선택
2. 해싱 기법 선택
: 키 충돌을 처리하는 방법
-> 위 두 가지 고려사항은 해시 테이블의 성능과 효율성에 크게 영향을 미침.
해시 함수
- 임의의 입력 키에 대해 정수 표현을 반환.
- 데이터베이스 해시 테이블에서는
암호화용 해시 함수(SHA-2등)를 사용하지 않는다. - 대신 빠르고 충돌률이 낮은 일반 목적 해시 함수 사용
해싱 기법 - Static Hashing Schemes
해싱 기법: 해시 테이블에서 충돌을 처리하는 기법
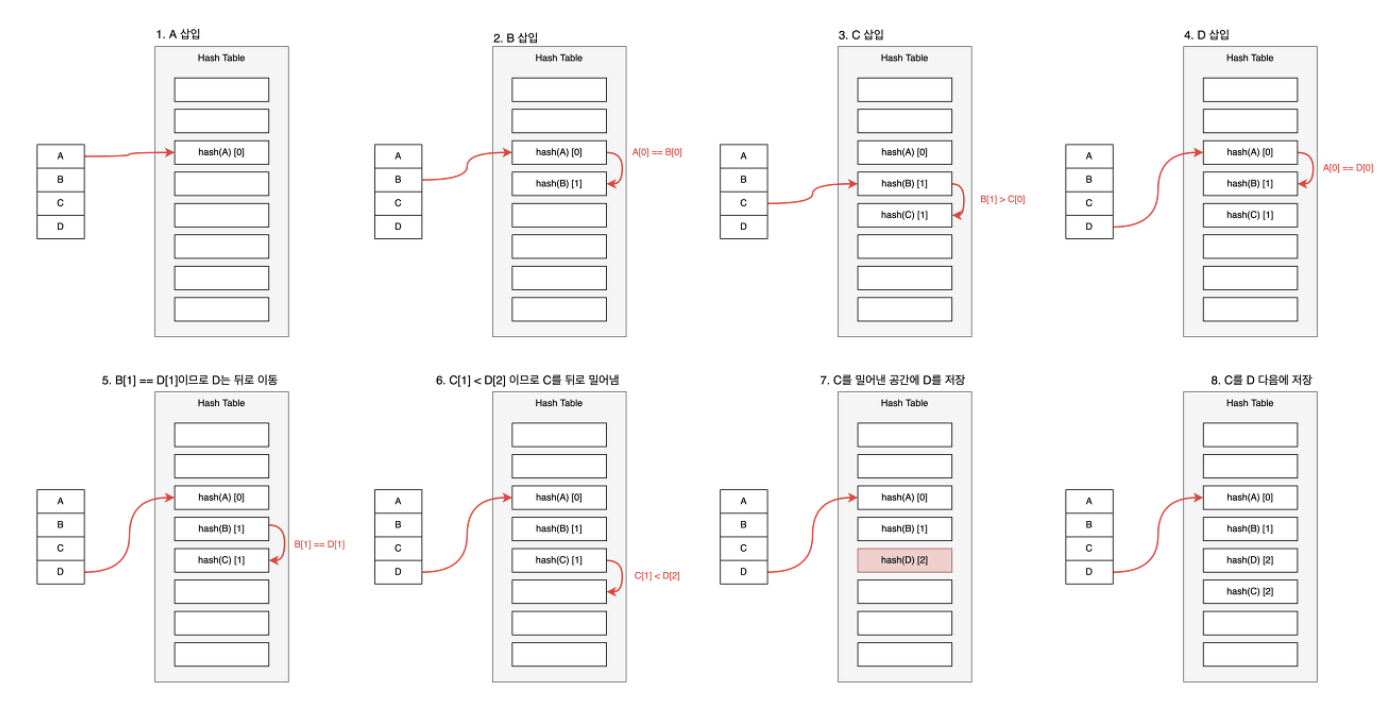
1. Linear Probe Hashing
- 단일 큰 테이블 사용
- 충돌 시 다음 빈 슬롯을 선형 검색
- 구현이 간단하고 메모리 오버헤드가 적다.
- 데이터가 클러스터링 되면 성능이 급격히 저하된다.
-> 이를 완화하게 위해 삭제 후 재해싱(Movement)이나 툼스톤(Tombstone) 기법을 사용.
- Movement
: 삭제된 슬롯 이후의 모든 요소를 재해싱하여 앞으로 이동시킨다. - Tombstone
: 삭제된 슬롯에 특별한 마커를 남겨두고,
새 키가 들어올 때 그 자리에 넣는다.
- Movement
- 간단하지만 충돌 처리가 비효율적이기 때문에
일반적으로 작은 데이터셋 이만 적합.
순서: 1. 키에 대한 해시 함수를 계산하여 넣을 배열의 초기 인덱스를 찾는다.
해시 함수=키% 테이블의 크기
2. 해당 인덱스가 비어있다면 키-값 쌍을 그 위치에 저장.
3. 해당 인덱스가 이미 차있다면, 다음 인덱스로 이동하여 비어 있는 슬롯을 찾는다
4. 끝까지 모든 인덱스를 찾아봤지만, 비어 있는 슬롯이 없다면,
테이블이 가득 찼다고 간주하고 오류를 내보낸다.
- 키가 유일하지 않은 경우

value값을 따로 저장.

구현이 쉽기 때문에 이 방법을 주로 사용한다.
2. Robin Hood Hashing
- 각 키는 원래 저장되어야 하는 슬롯 (최적 위치)으로부터 떨어진 거리를 함께 저장.
- 새로운 키의 최적 위치로부터의 거리 > 그 자리에 기존에 저장된 키의 최적 위치로부터의 거리
라면 기존 키를 밀어내고 그 위치에 새로운 키를 저장.
기존 키는 다음 자리에 저장. 채워져 있다면 그 키와 비교 - 아니라면 그다음에 빈 공간이 있다면 그곳에 저장.
그다음도 채워져 있다면 그 키와 비교
3. Cuckoo Hashing
- 여러 개의 해시 테이블(일반적으로 2개)과 서로 다른 해시 함수를 사용하는 기법
- 빈 슬롯이 있다면 키는 해당 슬롯에 저장.
- 빈 슬롯이 없다면 기존에 저장된 키를 제거하고 해당 키를 저장.
제거된 키는 다른 해시 테이블에 저장을 시도. - 삭제와 검색에 모두 상수 시간만큼만 소요

* 정적 해시 테이블의 한계 *
- 미리 해시 테이블의 크기를 정해야 한다.
- 저장할 키의 수를 미리 알고 있어야 한다.
- 각 키가 유일해야 하고, 완전한 해시 함수(perfect hash function)를 사용해야 한다.
- 하지만 실제 데이터베이스 시스템에서 만족되기 어렵다.
-> 데이터의 크기가 고정되어 있지 않고 변할 수 있기 때문.
-> 해결법: dynamic hash table 사용
Dynamic hash table
: 데이터의 수에 따라 자동으로 테이블의 크기를 조절한다.
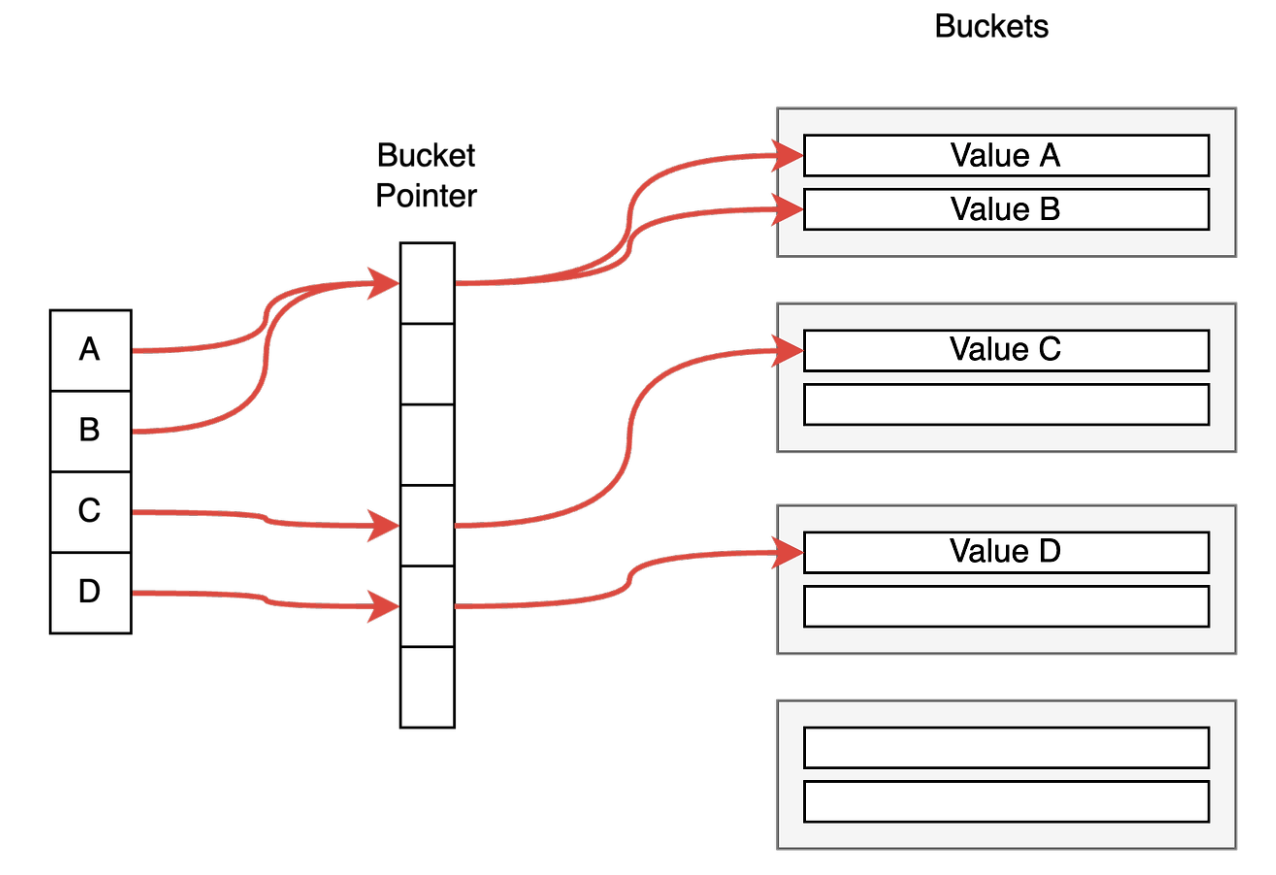
1. Chained Hashing
- 테이블의 각 슬롯은 linked list 형태의 bucket을 가리키는 포인터를 저장
- 동일한 해시키를 가진 값은 동일한 bucket에 저장
- 특정 데이터를 조회하기 위해서는
해당 해시 키를 통해 bucket을 찾고,
bucket에 저장된 데이터를 순차 탐색한다. - 삽입과 삭제의 성능은 bucket에 크기에 따라 달라진다.
2. Extendible Hashing
- Chained hashing의 경우 bucket의 linked list 수가 무한히 증가할 수 있다.
이것을 방지하기 위해 bucket을 분할하고 bit count를 통해 관리한다. - bit count를 증가시켜 bucket을 분할할 수 있다.
- 데이터의 재배치는 분할된 버킷 내에서만 이루어지므로 비용이 작다.
- 키가 유일하지 않아도 버킷 내 연결리스트로 처리할 수 있다.

기본 개념
1. global bit count: 해시 값의 처음 d개 비트 수
2. 각 버킷은 local bit count를 가진다.
global bit count보다 크지 않다.
3. 키의 접두사 비트를 해싱하여 들어갈 버킷을 결정한다.
접두사의 길이는 들어갈 버킷의 local bit count에 의해 결정된다.
4. 버킷이 가득 차면, 해당 버킷을 두 개로 분할하고,
local bit count를 1 증가시킨다.
5. 모든 버킷의 local bit count가 global bit count와 같아지면,
global bit count를 1 증가시킨다.
3. Linear Hashing
- 해시 테이블은 일련의 버킷들로 구성되어 있다.
- 모든 버킷은 동일한 크기를 가진다.
- 두 개의 해시 함수를 사용한다.
hash1(key)=key % N (N은 버킷의 수)
hash2(key)=key % (2*N) - split pointer: 다음에 split 될 버킷을 가리킨다.
- 버킷이 가득 차면, split pointer가 가리키는 버킷을 두 개로 분할한다.
기존 버킷의 값들은 hash2 함수를 사용하여 재분배된다. - split pointer가 마지막 슬롯에 도달하면
첫 번째 해시 함수를 삭제하고 다시 처음으로 이동한다. - 삭제와 검색은 상수 시간만큼 걸린다.
이해 안 가면 다음 링크 참고.
https://www.youtube.com/watch?v=h37Jhr21ByQ
삭제
1. 20이 어느 테이에 있나 찾는 중
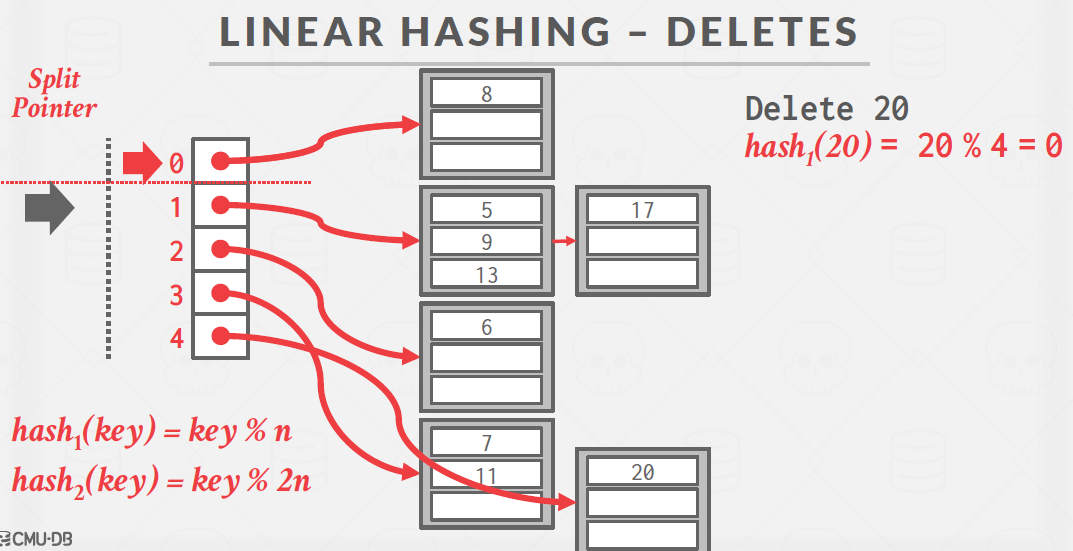

2. 삭제하고 해당 테이블에 값이 없다면 split pointer 한 칸 전으로 이동
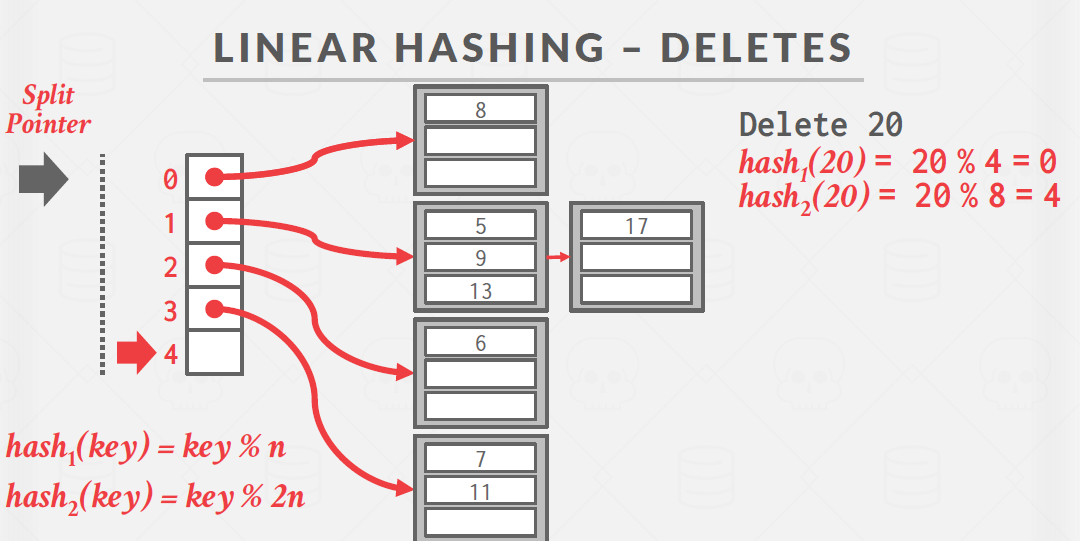
3. 4번 테이블 삭제

* Hash table의 한계*
정확한 값은 잘 가져오지만
범위로 값을 가져오고 싶을 때는 할 수 없다.
-> B+ tree로 보완
'데이터베이스' 카테고리의 다른 글
| B+ Tree Index (3) | 2024.06.11 |
|---|---|
| 7. Storage (1) (0) | 2024.05.01 |
| 6. Normalization (0) | 2024.04.16 |
| 5. E-R model (0) | 2024.04.08 |
| 4. Modern SQL (1) | 2024.04.02 |