Filtering in the Frequency Domain

Fourier's Idea

: 어느 함수든 다른 주파수들의 사인함수들의 합으로 표현 가능

 

 

 시간상의 시그널을 Fourier Transform을 하면 주기함수로 분해가능

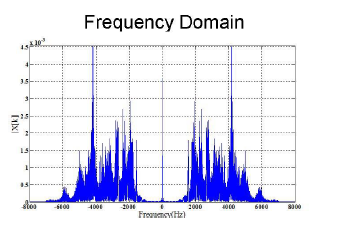
-> 그 크기대로 표현한 것
-> 어느 주파수를 많이 가지고 있구나를 파악 가능

 

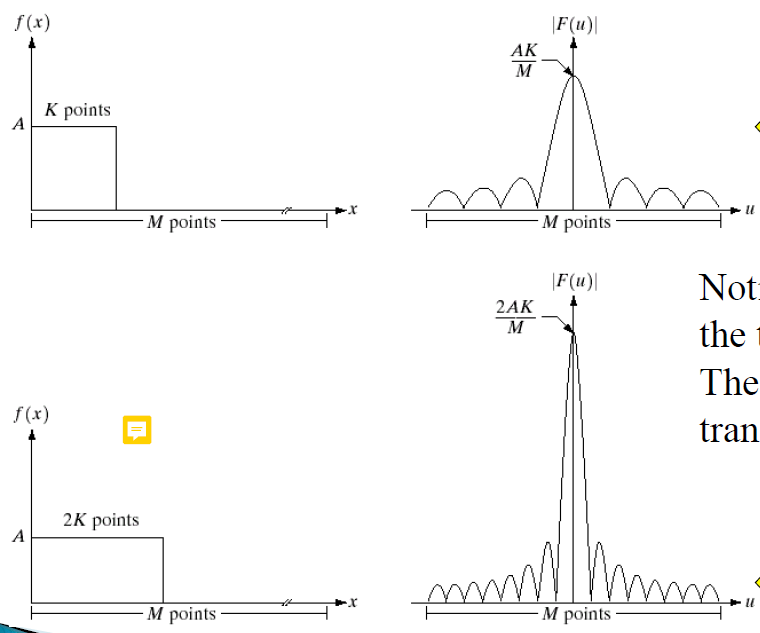
• 주기가 짧은 주기 함수
  -> 주파수가 높다
  ->높은 주파수 영역에 몰린다
• 주기가 긴 주기함수
  -> 주파수가 낮다
  -> 주파수가 작은 쪽에 에너지가 몰린다

 

 

2차원의 DFT

 

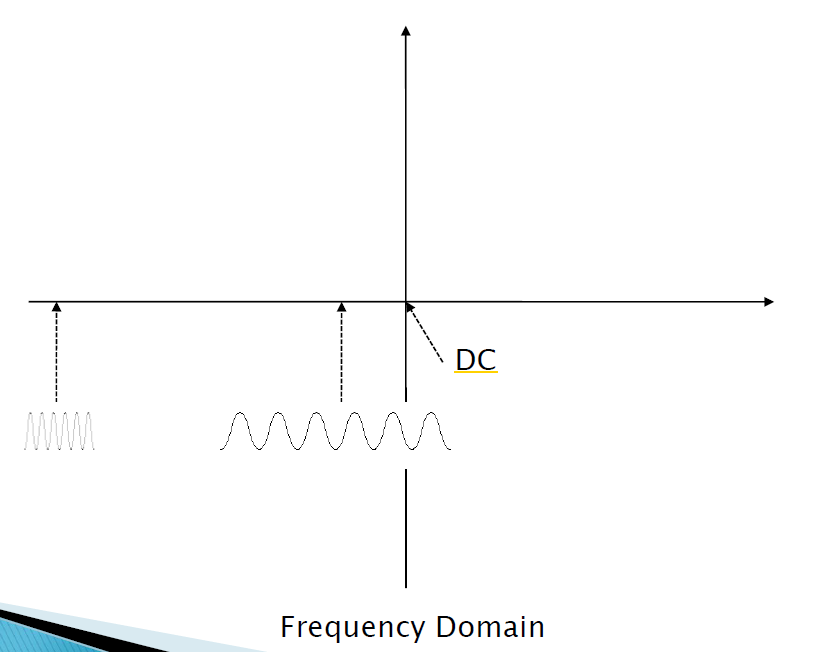
DC: 입력 데이터의 평균값

x축의 왼쪽으로 갈수록 주기가 짧은 함수

x축의 오른쪽으로 갈수록 주기가 긴 함수

 

 

2D DFT 취한것

• 어두운 부분: 높은 주파수가 없음
  -> 변화율이 낮음
• 밝은 부분: 높은 주파수가 많음
  -> 변화율이 높음
• 대각선으로 변하는 부분이 변화율이 커져서 밝음

 

 

주파수 도메인을 이용해서 filtering 하는 방법

1. Fourier transform하면 주파수 도메인 영상이 나옴

2. Filter function으로 필터링 한 후,

3. Inverse Fourier transform해서 되돌린다.

 

 

 

Image Smoothing Using Frequency Domain Filters

spatial domain에서는 한 점을 만들기 위해 convolution연산을 진행.
frequency domain에선 곱하기 연산으로 convolution연산을 대신 진행 
-> 단, LTI 시스템에서만 적용됨.

 

 

Lowpass Filters

: 주파수가 낮은 곳을 통과시키는 필터

-> 주파수 변화율이 적은 부분만 보겠다.

기준 주파수보다 낮은 곳은 1로 아닌 곳은 0으로

해당 주파수와 원점사이의 거리 계산

 

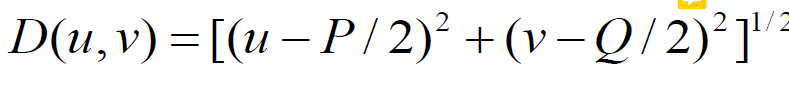
원의 크기가 커질수록 주기가 짧은 함수들 표현 가능

-> 변화율이 큰 주파수 표현 가능

 

 

Lowpass filter 종류

1. Butterworth Lowpass Filters

Butterworth가 조금더 선명함, 물결무늬(ringing)가 안보임

 

2. Gaussian Lowpass Filters

 

 

 

High Pass filters

: low pass filters의 반대

높은 주파수만 통과시킨다.

1-low pass filter로 구한다.