2023. 11. 10. 21:46ㆍ컴퓨터비전
Noise
: 영상의 픽셀값에 추가되는 원치 않는 형태의 신호를 의미
1. Salt-and pepper noise
: 픽셀값들의 일부가 무작위 값으로 대체되는 경우이다.
salt noise는 픽셀이 하얀색인 경우이고,
pepper noise는 픽셀이 검정색인 경우

2. Gaussian noise
: 원래의 픽셀값이 아닌 오차가 생긴 값이 들어가는 경우이다.
평균이 0이고, 표준 편차가 1인 가우시안 분포를 정상 분포라고도 한다.

노이즈 제거하기
1. Median Filter
- non linear filter
- 픽셀값을 kenel 값들을 정렬한 상태에서 중간값을 선택하는 방식
-> 중간에서 멀리 떨어진 값들은 선택되지 않아
salt-and-pepper noise를 제거하는데 효과적으로 사용된다.

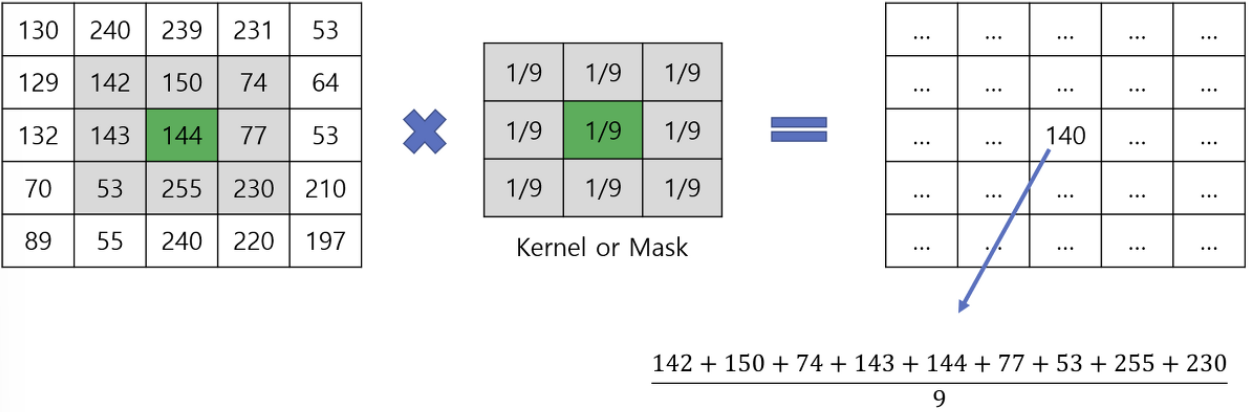
2. Mean Filter
- 픽셀값을 주위 픽셀들의 평균 값으로 대체하는 방식
- kernel(mask)이 3*3이라면
#include <opencv2/opencv.hpp>
#include <vector>
#include <algorithm>
#include <numeric>
using namespace cv;
using namespace std;
Mat MedianFilter(const Mat& img, int ksize) {
int center = ksize / 2; //중심 픽셀로부터 커버할 픽셀까지의 거리
Mat filter = img.clone();
for (int y = center;y < filter.rows - center;y++) {
for (int x = center;x < filter.cols - center;x++) {
vector<uchar> near;
for (int i = -center;i <= center;i++) {
for (int j = -center;j <= center;j++) {
near.push_back(img.at<uchar>(y + i, x + j)); //3*3픽셀들 벡터에 담기
}
}
sort(near.begin(), near.end()); //3*3 픽셀들 정렬
filter.at<uchar>(y, x) = near[near.size() / 2]; //중간값으로 픽셀값 설정
}
}
return filter;
}
Mat MeanFilter(const Mat& img, int ksize) {
int center = ksize / 2; //중심 픽셀로부터 커버할 픽셀까지의 거리
Mat filter = img.clone();
for (int y = center;y < filter.rows - center;y++) {
for (int x = center;x < filter.cols - center;x++) {
vector<uchar> near;
for (int i = -center;i <= center;i++) {
for (int j = -center;j <= center;j++) {
near.push_back(img.at<uchar>(y + i, x + j)); //3*3픽셀들 벡터에 담기
}
}
float sum =accumulate(near.begin(), near.end(),0.0); //픽셀값들 누적합 구하기
filter.at<uchar>(y, x) = sum/near.size(); //평균값으로 픽셀값 설정
}
}
return filter;
}
int main() {
Mat image = imread("Lena512.jpg",IMREAD_GRAYSCALE);
//imshow("input", image); //원본 이미지
Mat noise1(image.size(), CV_8U);
randn(noise1, 0, 15); //평균이 0,표준편차가 15인 가우시안 분포를 따르는 난수 생성(적은 가우시안 노이즈 생성)
Mat noise2(image.size(), CV_8U);
randn(noise2, 0, 30); //평균이 0,표준편차가 15인 가우시안 분포를 따르는 난수 생성(큰 가우시안 노이즈 생성)
Mat result1, result2;
add(image, noise1, result1, Mat(), CV_8U); //원본에 가우시안 노이즈 합치기,0~255범위 벗어나지 않도록 합치기
add(image, noise2, result2, Mat(), CV_8U);
Mat result3 = image.clone();
Mat result4 = image.clone();
int num1 = (int)(image.total() * 0.05); //0.05 확률로 salt&pepper noise 만들기
for (int i = 0;i < num1;i++) {
int x = rand() % result3.cols;
int y = rand() % result3.rows;
result3.at<uchar>(y, x) = (i % 2) * 255;
}
int num2 = (int)(image.total() * 0.1); //0.1 확률로 salt&pepper noise 만들기
for (int i = 0;i < num2;i++) {
int x = rand() % result4.cols;
int y = rand() % result4.rows;
result4.at<uchar>(y, x) = (i % 2) * 255;
}
imshow("gaussian_noise=10", result1); //표준편차가 10인 가우시안 노이즈
imshow("gaussian_noise=30", result2); //표준편차가 30인 가우시안 노이즈
imshow("salt&pepper: 0.05", result3); //0.05확률의 salt&pepper 노이즈
imshow("salt&pepper: 0.1", result4); //0.1확률의 salt&pepper 노이즈
//각각에 median_filter 적용
imshow("median-10", MedianFilter(result1, 3));
imshow("median-30", MedianFilter(result2, 3));
imshow("median-0.05", MedianFilter(result3, 3));
imshow("median-0.1", MedianFilter(result4, 3));
//각각에 mean_filter 적용
imshow("mean-10", MeanFilter(result1, 3));
imshow("mean-30", MeanFilter(result2, 3));
imshow("mean-0.05", MeanFilter(result3, 3));
imshow("mean-0.1", MeanFilter(result4, 3));
waitKey(0);
return 0;
}
Adaptive Filters
: 이미지의 특성에 맞게 적용하는 필터

다음과 같이 변수들을 정의할 때,
- 2번 변수가 0이라면 : 노이즈가 없는 상태이므로 그냥 g(x,y) 반환하면 된다.
- 4번 변수가 2번 변수에 비해 높은경우라면 : edge가 존재할 것.
->원래 영상의 변화가 커서 필터를 세게 적용하면 안된다.
-> g(x,y)에 가까운 값 반환 - 4번 변수와 2번 변수가 같은 경우라면
: S(x,y) 윈도우 내에 전체 영상에 부가된 noise와 동일한 분포로 포함되어 있다.
-> 필터를 강하게 적용해도 된다.
-> 평균을 구해 노이즈 감쇠
Adaptive Median Filter
Level A:
A1=Z(median) - Z(min)
A2=Z(median) - Z(max)
if A1>0,A2<0이라면 Level B로 이동 //이걸 만족하면 median값이 노이즈가 아닌것으로 판단
else 윈도우 사이즈 키우기 //아니라면 일단 좀더 넓은 범위에서 탐색해보기
if 윈도우 크기 <= 윈도우 크기최대치라면 Level A 반복
else Z(xy) 반환 //픽셀값을 median값으로 대체
Level B:
B1=Z(xy) - Z(min)
B2=Z(xy) - Z(max)
if B1>0, B2<0이라면 Z(xy)반환 //노이즈가 없는 상태이므로 자기자신 반환
else Z(median) 반환 //노이즈가 있는 상태이므로 중간값 반환

확실히 3번째가 엣지 디테일을 많이 살려 복원한다.
Inverse Filter
g(x,y)는 degraded image
f(x,y)는 original image
n(x,y)는 noise
h(x,y)는 filter일 때
Spatial domain: g(x,y)=f(x,y)*h(x,y)+n(x,y)
-> Frequency domain : G(u,v)=F(u,v)H(u,v) +N(u,v)
F^(u,v)(복원된 영상) = G(u,v)/H(u,v) = F(u,v)+N(u,v)/H(u,v)
: H값이 작을 때는 노이즈값이 커서 괜찮은데
H값이 커질 때는 노이즈값이 작아져서 값이 이상해짐
-> lowpass filter로 해결가능

통과 filter의 반지름이 커질수록 이상한값이 나온다.
'컴퓨터비전' 카테고리의 다른 글
| Feature Detection and Matching (0) | 2023.11.14 |
|---|---|
| Edge Detection (0) | 2023.11.12 |
| (opencv) visual studio에 적용하기 (0) | 2023.11.01 |
| Filtering in the Frequency Domain (1) | 2023.10.18 |
| Filtering (1) | 2023.10.18 |