2023. 10. 14. 21:26ㆍ컴퓨터비전
Image size ( resolution) : M * N
Intensity level(밝기 레벨) : 0~255, 8 bit로 표현
Gray Image
- 1 pixel: 1 byte
- M*N pixel= M*N*1 bytes
Color Image(R,G,B)
- 1 pixel: 3 bytes
- M*N pixel= M*N*3 bytes
Gray Levels
회색도: 명암을 표현하는 수
Quantization
양자화: 실수형 변수(floating-point type)를 정수형 변수(integer or fixed point)로 변환하는 과정
Sampling
: 연속적인 신호(함수)에서 특정 위치를 대표하는 값을 뽑아내는 과정
Aliasing
: Sampling 된 값을 다시 연속적인 값으로 복원할 떄, 기존의 신호와 달라지는 현상
Interpolation
: 보간. 해상도 보완
새로운 점을 만들기 위해 수많은 점들을 평균화시키는 것.
Pixel Add/Sub
- pixel값은 0보단 작을 수 없고 2^n-1보다 클 수 없다
- 예) 128+255=255
128-255=0
Linear
-> H(Img1+Img2)=H(Img1)+H(Img2)
Non-Linear
-> H(Img1+Img2)!=H(Img1)+H(Img2)
Image Interpolation할 때
회전을 하고 interpolation을 하는 게 편하다.
2배 확대 2배 축소-> 원래대로 돌아감
1.7배 확대 1.7배 축소-> 안돌아감, 해상도 저하가 생김
Bilinear Interpolation
: 직선으로 예측
Bicubic Interpolation
: 곡선으로 예측
Edge-Directed Interpolation
: 엣지를 살리면서
이미지 회전시키기

1. 입력영상과 같은 크기의 이미지 생성
2. output(x,y) - (W/2,H/2) =A
(역방향으로 맵핑해야 이미지에 빵꾸가 안생긴다)
2.

input(x,y) =R(세타) * A
(세타는 라디안값으로 넣어줘야 한다)
3. input(x,y)+(W/2,H/2)=B
4. 이제 output(x,y)에 B 위치의 픽셀값들을 하나씩 맵핑한다.
(단, 이미지를 벗어나는 좌표는 건너뜀)
Bilinear Interpolation
원 이미지를 N배 확대하는 경우, 새로 만들어지는 결과 이미지에는
원 이미지의 값을 받지 못하는 빈 픽셀들이 생긴다.
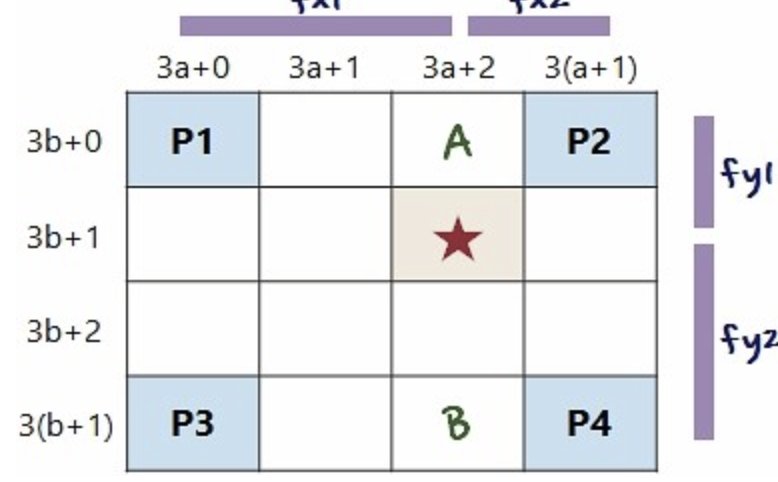
3배 확대한다고 가정하면, 파란색 픽셀들이 원 영상으로부터 값을 받게 되는 부부닝고
나머지 흰 픽셀들을 추정해야 한다
이것이 보간법(interpolation)이다.
1.
구하고자 하는 별표의 좌표를 (y,x)라, output의 좌표를 (Y,X)라 가정
2.
(y,x)와 인접한 4개의 점을 원래 이미지로부터 찾는다.
3.
p1좌표= (Y/3, X/3)
p2= (Y/3, X/3+1)
p3= (Y/3+1, X/3)
p4= (Y/3+1, X/3+1)
4.
4개의 점과 별표사이의 거리비 구하기
fx1=(x-X/3)
fx2=1-fx1
fy1=(y=Y/3)
fy2=1-fy1
5. linear interpolation을 x축에 대하여 적용
p1과 p2의 픽셀값과 거리비로 A의 픽셀값 구하기
A= p1의 픽셀값 * fx2 + p2의 픽셀값 * fx1
B=p3의 픽셀값 * fx2 + p4의 픽셀값 * fx1
6. linear interpolation을 y축에 대하여 적용
A와 B의 픽셀값과 거리비로 별표의 픽셀값 구하기
=A * fy2 + B * fy1
'컴퓨터비전' 카테고리의 다른 글
| Filtering in the Frequency Domain (1) | 2023.10.18 |
|---|---|
| Filtering (1) | 2023.10.18 |
| Color Image (0) | 2023.10.17 |
| Intensity Transform (2) | 2023.10.15 |
| Fundamentals of signal Processing (2) | 2023.10.14 |